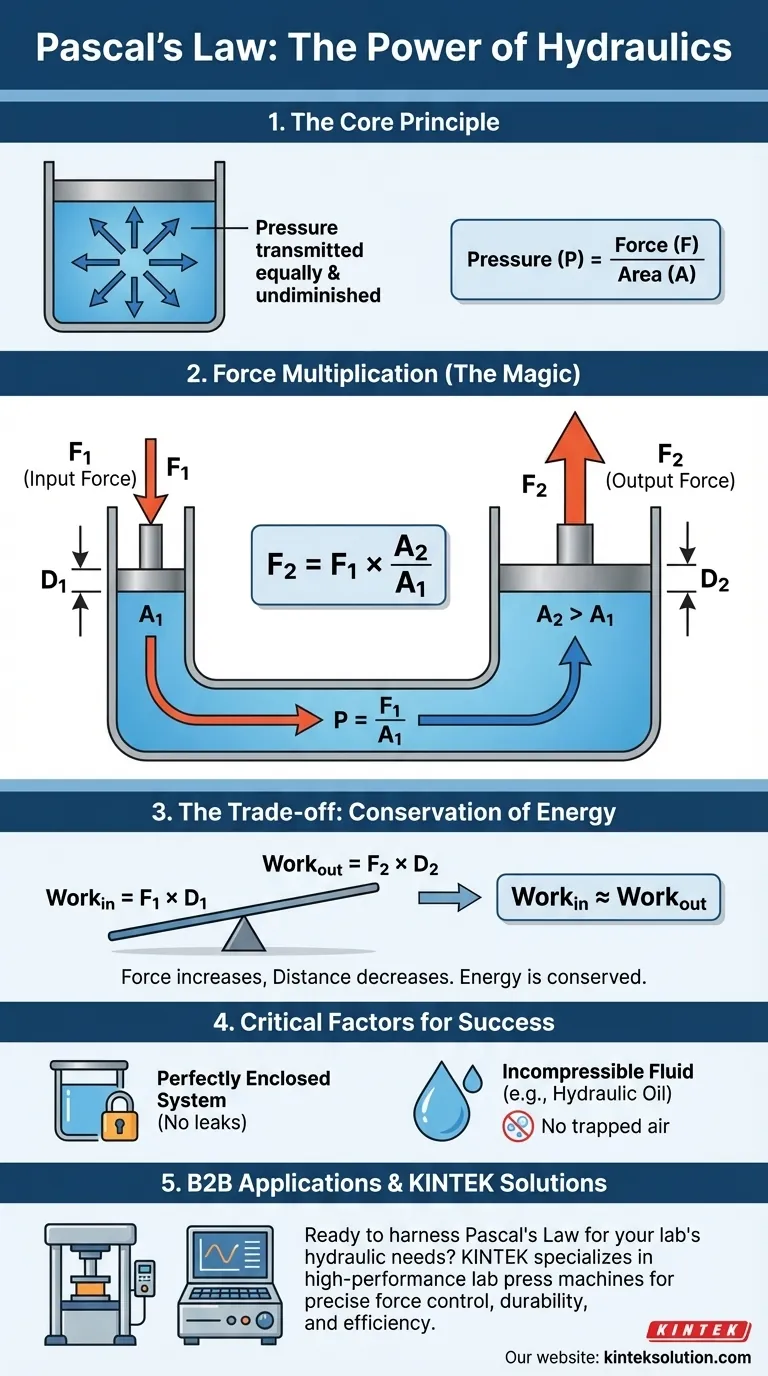
Im Kern besagt das Pascalsche Gesetz, dass eine Druckänderung an jedem Punkt in einer eingeschlossenen, inkompressiblen Flüssigkeit gleichmäßig und ungemindert auf alle Teile dieser Flüssigkeit übertragen wird. Das bedeutet, wenn Sie auf eine Flüssigkeit in einem geschlossenen Behälter drücken, steigt der Druck überall in diesem Behälter um genau den gleichen Betrag und zur exakt gleichen Zeit.
Während sich die Definition auf die Druckübertragung konzentriert, liegt die wahre Kraft des Pascalschen Gesetzes darin, wie es uns ermöglicht, eine massive Kraftvervielfachung zu erreichen. Dieses einzige Prinzip ist die Grundlage fast aller modernen Hydrauliksysteme.
Die grundlegende Gleichung: Druck, Kraft und Fläche
Um die Auswirkungen des Pascalschen Gesetzes zu verstehen, müssen Sie zunächst die Beziehung zwischen seinen drei Kernkomponenten verstehen.
Druck definieren
Druck (P) ist definiert als eine Kraft (F), die auf eine bestimmte Fläche (A) ausgeübt wird. Die Gleichung lautet P = F/A.
Denken Sie an den Unterschied, ob Sie jemand mit offener Handfläche oder mit einem einzigen Finger drückt. Die Kraft mag die gleiche sein, aber der Druck von der Fingerspitze ist weitaus größer, weil er auf eine viel kleinere Fläche konzentriert ist.
Die Rolle einer inkompressiblen Flüssigkeit
Das Pascalsche Gesetz beruht auf der Verwendung einer inkompressiblen Flüssigkeit, wie Wasser oder Hydrauliköl. Wenn Sie Kraft auf diese Art von Flüssigkeit ausüben, wird sie nicht in ein kleineres Volumen gepresst.
Da die Flüssigkeit nicht komprimiert werden kann, muss die von Ihnen eingebrachte Energie woanders übertragen werden. So breitet sich der Druck sofort im gesamten System aus.
Die Magie der Kraftvervielfachung
Das wahre Genie der Anwendung des Pascalschen Gesetzes liegt nicht nur darin, dass Druck übertragen wird, sondern dass er zur Kraftvervielfachung genutzt werden kann. Dies ist das Funktionsprinzip hinter allem, vom Wagenheber bis zum Fahrwerk eines Flugzeugs.
Das grundlegende Hydraulikmodell
Stellen Sie sich ein U-förmiges Rohr vor, das mit Öl gefüllt und an beiden Enden durch Kolben verschlossen ist. Ein Kolben ist klein (der Eingangskolben), und der andere ist groß (der Ausgangskolben).
Die Eingangskraft anwenden
Nehmen wir an, Sie üben eine kleine abwärts gerichtete Kraft (F1) auf den kleinen Kolben aus, der eine Fläche A1 hat. Dies erzeugt einen Druck in der Flüssigkeit: P = F1 / A1.
Den Druck übertragen
Nach dem Pascalschen Gesetz ist dieser exakte Druck (P) nun überall in der Flüssigkeit vorhanden. Dies schließt den Bereich direkt unter dem großen Ausgangskolben ein.
Die Ausgangskraft berechnen
Dieser gleiche Druck (P) drückt nun nach oben auf den großen Kolben, der eine Fläche A2 hat. Die resultierende Aufwärtskraft (F2) ist F2 = P x A2.
Da der Druck überall gleich ist (F1/A1 = F2/A2), können Sie sehen, dass die Ausgangskraft proportional zum Verhältnis der Flächen ist. Wenn die Fläche des Ausgangskolbens 10-mal größer ist als die Fläche des Eingangskolbens, ist die Ausgangskraft 10-mal größer als die von Ihnen ausgeübte Kraft.
Die Abwägungen verstehen
Diese Kraftvervielfachung kommt nicht aus dem Nichts; sie folgt den Gesetzen der Physik und beinhaltet entscheidende Kompromisse.
Energieerhaltung
Man kann keine Energie aus dem Nichts erzeugen. Während die Ausgangskraft vervielfacht wird, wird der Weg, den der Ausgangskolben zurücklegt, proportional reduziert.
Um den großen Kolben um 1 Zoll anzuheben, müssen Sie den kleinen Kolben möglicherweise um 10 Zoll nach unten drücken. Die geleistete Arbeit (Kraft x Weg) bleibt auf beiden Seiten gleich, Reibung ignoriert.
Die Bedeutung eines „geschlossenen“ Systems
Das Pascalsche Prinzip funktioniert nur in einem perfekt abgedichteten System. Jede Leckage würde dazu führen, dass die Flüssigkeit beim Anlegen von Druck entweicht, wodurch der Druck abgebaut wird und es zu einem Systemausfall kommt.
Flüssigkeitseigenschaften sind wichtig
Während wir oft von einer idealen, inkompressiblen Flüssigkeit ausgehen, haben reale Hydraulikflüssigkeiten Viskosität (Widerstand gegen Fließen) und können eingeschlossene Luftblasen enthalten. Luft ist stark komprimierbar, und ihre Anwesenheit in Hydraulikleitungen kann das System „schwammig“ erscheinen lassen und seine Effizienz dramatisch reduzieren.
Wie Sie dies auf Ihr Projekt anwenden
Das Verständnis des Prinzips ermöglicht es Ihnen, Systeme effektiv zu entwerfen und Fehler zu beheben. Ihr spezifisches Ziel bestimmt, welcher Aspekt des Gesetzes am wichtigsten ist.
- Wenn Ihr Hauptaugenmerk auf mechanischen Vorteilen liegt: Konzentrieren Sie sich darauf, das Flächenverhältnis zwischen Ausgangs- und Eingangskolben (A2/A1) zu maximieren, um die gewünschte Kraftvervielfachung für eine Presse oder einen Hebeheber zu erreichen.
- Wenn Ihr Hauptaugenmerk auf Systemeffizienz liegt: Priorisieren Sie die Schaffung eines perfekt abgedichteten Systems und die Verwendung einer hochwertigen, inkompressiblen Flüssigkeit, um Energieverluste durch Lecks oder interne Kompression zu minimieren.
- Wenn Ihr Hauptaugenmerk auf Präzisionssteuerung liegt: Nutzen Sie den Arbeitstausch; eine kleine, beherrschbare Bewegung am Eingang kann sich in eine sehr kleine, aber leistungsstarke und präzise Bewegung am Ausgang übersetzen, was ideal für Systeme wie Fahrzeugbremsen ist.
Indem Sie dieses Prinzip verstehen, gehen Sie von der bloßen Kenntnis einer Definition zum Erfassen der eleganten Kraft hinter der gesamten Hydrauliktechnik über.
Zusammenfassungstabelle:
| Aspekt | Wichtige Erkenntnis |
|---|---|
| Definition | Druckänderung in inkompressibler Flüssigkeit wird gleichmäßig und ungemindert übertragen. |
| Kraftvervielfachung | Ausgangskraft steigt mit dem Flächenverhältnis (F2 = F1 × (A2/A1)). |
| Abwägungen | Kraftgewinn reduziert den zurückgelegten Weg; Energie wird konserviert. |
| Anwendungen | Verwendung in Hydraulikhebern, Pressen und Präzisionssteuerungssystemen. |
Bereit, das Pascalsche Gesetz für die hydraulischen Anforderungen Ihres Labors zu nutzen? KINTEK ist spezialisiert auf Hochleistungs-Laborpressenmaschinen, einschließlich automatischer Laborpressen, isostatischer Pressen und beheizter Laborpressen. Unsere Geräte gewährleisten präzise Kraftkontrolle, Haltbarkeit und Effizienz für Ihre Laboranwendungen. Kontaktieren Sie uns noch heute, um zu besprechen, wie unsere Lösungen Ihre Projekte optimieren und die Produktivität steigern können!
Visuelle Anleitung
Ähnliche Produkte
- Automatische hydraulische Laborpresse zum Pressen von XRF- und KBR-Granulat
- Manuell beheizte hydraulische Laborpresse mit integrierten Heizplatten Hydraulische Pressmaschine
- Automatische beheizte hydraulische Pressmaschine mit heißen Platten für das Labor
- Automatische beheizte hydraulische Pressmaschine mit beheizten Platten für das Labor
- Hydraulische Laborpresse Laborgranulatpresse für Handschuhfach
Andere fragen auch
- Wie werden hydraulische Pressen bei der Probenvorbereitung im Labor eingesetzt? Genaue Analysen mit homogenen Proben sicherstellen
- Wie gewährleisten hydraulische Pressen Präzision und Konsistenz bei der Druckausübung?Erreichen Sie eine zuverlässige Kraftkontrolle für Ihr Labor
- Welche Vorteile bietet das Pressen von Proben zu Pellets für die RFA-Analyse? Steigerung von Genauigkeit und Reproduzierbarkeit
- Was sind die Vorteile der Verwendung von Handpressen in Laboren? Steigern Sie Präzision und Effizienz in Ihrem Labor
- Wie schneiden gepresste Pellets im Vergleich zu anderen Probenvorbereitungsmethoden für die RFA-Analyse ab? Steigern Sie Genauigkeit und Effizienz in Ihrem Labor
