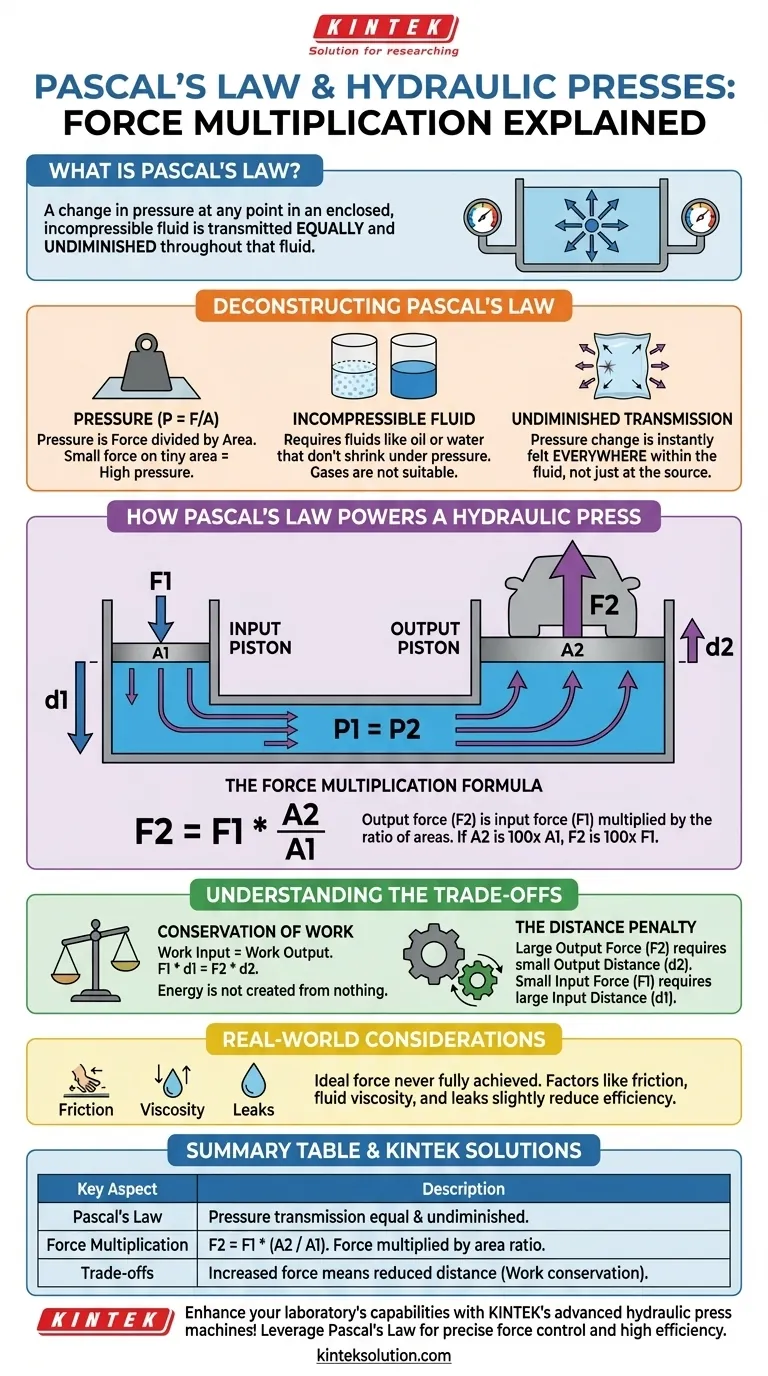
Im Kern besagt das Pascalsche Gesetz, dass eine Druckänderung an einem beliebigen Punkt in einer eingeschlossenen, inkompressiblen Flüssigkeit sich gleichmäßig und ungeschwächt in der gesamten Flüssigkeit ausbreitet. Dieses Prinzip ist der grundlegende Mechanismus hinter hydraulischen Pressen, der es ermöglicht, eine kleine, handhabbare Kraft in eine immens starke umzuwandeln. Es funktioniert, indem dieser anfängliche Druck über eine viel größere Fläche übertragen wird, wodurch die resultierende Kraft vervielfacht wird.
Die zentrale Erkenntnis des Pascalschen Gesetzes ist, dass man Kraft nicht aus dem Nichts erzeugt. Stattdessen verwendet man eine inkompressible Flüssigkeit, um den Druck gleichmäßig zu übertragen, wodurch eine kleine Kraft auf eine kleine Fläche einen äquivalenten Druck erzeugt, der auf eine größere Fläche wirkt und so eine größere Gesamtkraft zur Folge hat.
Das Pascalsche Gesetz dekonstruieren
Um wirklich zu verstehen, wie hydraulische Systeme funktionieren, müssen wir zunächst die drei Kernkomponenten des Prinzips selbst verstehen.
Die Definition von Druck
Druck (P) ist definiert als eine Kraft (F), die über eine bestimmte Fläche (A) ausgeübt wird. Die Beziehung wird durch die Grundgleichung P = F/A ausgedrückt.
Eine kleine Kraft, die auf eine winzige Fläche konzentriert ist, kann denselben Druck erzeugen wie eine massive Kraft, die sich über eine große Fläche verteilt. Dieses Konzept ist der Schlüssel zum Verständnis der Kraftverstärkung.
Die inkompressible Flüssigkeit
Das Pascalsche Gesetz erfordert eine inkompressible Flüssigkeit, wie Öl oder Wasser. Das bedeutet, dass sich das Volumen der Flüssigkeit bei Druckbeaufschlagung nicht merklich verringert.
Gase sind kompressibel und würden sich unter Druck einfach verdichten, anstatt ihn effizient zu übertragen, wodurch sie für diese Anwendung ungeeignet wären.
Ungeschwächte Übertragung
Dies ist der kritischste Aspekt des Gesetzes. Wenn Sie Druck auf einen beliebigen Teil der eingeschlossenen Flüssigkeit ausüben, wird genau derselbe Druck sofort überall innerhalb der Flüssigkeit wahrgenommen.
Stellen Sie sich einen versiegelten Plastikbeutel voller Wasser vor. Wenn Sie ihn an einer Stelle mit dem Finger anstechen, wird der gesamte Beutel straff, und der Druck steigt überall gleichermaßen an, nicht nur dort, wo Ihr Finger ist.
Wie das Pascalsche Gesetz eine hydraulische Presse antreibt
Eine hydraulische Presse ist die klassische, praktische Anwendung dieses Prinzips. Sie verwendet ein einfaches Zwei-Kolben-System, um eine erhebliche Kraftverstärkung zu erzielen.
Das Zwei-Kolben-System
Ein grundlegendes Hydrauliksystem besteht aus zwei zylindrischen Kolben, die durch eine mit einer inkompressiblen Flüssigkeit gefüllte Leitung verbunden sind.
- Kolben 1 (Eingang): Hat eine kleine Oberfläche (
A1). - Kolben 2 (Ausgang): Hat eine viel größere Oberfläche (
A2).
Eine kleine Eingangskraft (F1) wird auf Kolben 1 ausgeübt, wodurch ein Druck in der Flüssigkeit erzeugt wird.
Gleicher Druck, ungleiche Kraft
Nach dem Pascalschen Gesetz wird der vom Eingangskolben erzeugte Druck (P1 = F1 / A1) ungeschwächt durch die Flüssigkeit übertragen. Das bedeutet, dass der auf den Ausgangskolben wirkende Druck (P2) exakt derselbe ist.
Daher gilt: P1 = P2.
Weil P = F/A ist, können wir substituieren, um die Gleichung zu erhalten: F1 / A1 = F2 / A2.
Die Kraftverstärkungsformel
Durch Umstellen der Gleichung können wir die Ausgangskraft (F2) lösen:
F2 = F1 * (A2 / A1)
Dies demonstriert elegant den Multiplikationseffekt. Die Ausgangskraft ist die Eingangskraft multipliziert mit dem Verhältnis der Flächen der beiden Kolben. Wenn die Fläche des Ausgangskolbens 100-mal größer ist als die Fläche des Eingangskolbens, wird die Kraft um das 100-fache vervielfacht.
Die Kompromisse verstehen
Dieses Prinzip erzeugt keine Energie aus dem Nichts. Die verstärkte Kraft hat ihren Preis, der durch den Energieerhaltungssatz bestimmt wird.
Die Energieerhaltung der Arbeit
In der Physik gilt: Arbeit = Kraft x Weg. Damit ein Hydrauliksystem im Gleichgewicht ist, muss die am Eingangskolben verrichtete Arbeit der vom Ausgangskolben verrichteten Arbeit entsprechen.
Arbeit_Eingang = Arbeit_Ausgang
F1 * d1 = F2 * d2
Der Distanz-Nachteil
Da die Ausgangskraft (F2) viel größer ist als die Eingangskraft (F1), muss der Weg, den der Ausgangskolben zurücklegt (d2), proportional kleiner sein als der Weg, den der Eingangskolben zurücklegt (d1).
Um ein schweres Auto mit dem großen Kolben um einen Zoll anzuheben, müssen Sie den kleinen Kolben möglicherweise über eine Distanz von mehreren Fuß drücken. Sie tauschen Bewegungsdistanz gegen Kraftverstärkung ein.
Ineffizienzen in der realen Welt
Bei jeder praktischen Anwendung wird die ideale Ausgangskraft nie vollständig erreicht. Faktoren wie Reibung zwischen Kolben und Zylinderwänden, Fluidviskosität und potenzielle Leckagen im System verringern alle die Effizienz der Kraftübertragung geringfügig.
Die richtige Wahl für Ihr Ziel treffen
Das Verständnis dieses Prinzips ermöglicht es Ihnen, gezielte Designentscheidungen basierend auf Ihrem primären Ziel zu treffen.
- Wenn Ihr Hauptaugenmerk auf maximaler Kraftverstärkung liegt: Sie müssen das Verhältnis der Ausgangsfläche (
A2) zur Eingangsfläche (A1) maximieren. - Wenn Ihr Hauptaugenmerk auf Betriebsgeschwindigkeit liegt: Sie müssen ein geringeres Kraftverstärkungsverhältnis in Kauf nehmen, da ein größerer Ausgangsweg (
d2) ein kleineres Flächenverhältnis (A2/A1) erfordert. - Wenn Sie ein reales System entwerfen: Berücksichtigen Sie immer eine Marge für Ineffizienz; die tatsächliche Ausgangskraft wird aufgrund von Reibung und anderen Verlusten geringfügig unter der theoretischen Berechnung liegen.
Letztendlich bietet das Pascalsche Gesetz einen leistungsstarken und eleganten Rahmen, der ein Eckpfeiler der modernen Maschinenbau- und Industrietechnik bleibt.
Zusammenfassungstabelle:
| Schlüsselaspekt | Beschreibung |
|---|---|
| Pascalsches Gesetz | Druckänderungen in einer inkompressiblen Flüssigkeit werden gleichmäßig und ungeschwächt in der gesamten Flüssigkeit übertragen. |
| Formel zur Kraftverstärkung | F2 = F1 * (A2 / A1), wobei F2 die Ausgangskraft, F1 die Eingangskraft, A2 die Ausgangsfläche und A1 die Eingangsfläche ist. |
| Kompromisse | Erhöhte Kraft geht einher mit reduziertem Weg, gesteuert durch den Energieerhaltungssatz (F1 * d1 = F2 * d2). |
| Anwendungen | Ideal für hydraulische Pressen in Laboren, die präzise Steuerung und hohe Kraft für Materialtests und -verarbeitung bieten. |
Verbessern Sie die Leistungsfähigkeit Ihres Labors mit den fortschrittlichen hydraulischen Pressmaschinen von KINTEK! Ob Sie eine automatische Laborpresse, eine isostatische Presse oder eine beheizte Laborpresse benötigen, unsere Geräte nutzen das Pascalsche Gesetz, um präzise Kraftsteuerung, hohe Effizienz und zuverlässige Leistung für alle Ihre Laboranforderungen zu liefern. Lassen Sie sich nicht von Ineffizienzen zurückhalten – kontaktieren Sie uns noch heute, um zu erfahren, wie unsere Lösungen Ihre Produktivität steigern und überlegene Ergebnisse bei Materialtests und -verarbeitung erzielen können!
Visuelle Anleitung
Ähnliche Produkte
- Hydraulische Laborpresse 2T Labor-Pelletpresse für KBR FTIR
- Labor-Hydraulikpresse Labor-Pelletpresse Knopf-Batterie-Presse
- Automatische hydraulische Laborpresse Labor-Pressmaschine für Pellets
- Manuell beheizte hydraulische Laborpresse mit integrierten Heizplatten Hydraulische Pressmaschine
- Manuelle Labor-Hydraulikpresse Labor-Pelletpresse
Andere fragen auch
- Wie gewährleisten hydraulische Pressen Präzision und Konsistenz bei der Druckausübung?Erreichen Sie eine zuverlässige Kraftkontrolle für Ihr Labor
- Wie werden hydraulische Pressen in der Spektroskopie und der Zusammensetzungsbestimmung eingesetzt? Verbesserung der Genauigkeit bei FTIR- und RFA-Analysen
- Wie wird eine hydraulische Presse bei der Probenvorbereitung für die Spektroskopie eingesetzt?Genaue und homogene Probenpellets erzielen
- Was sind die Hauptvorteile des Einsatzes von hydraulischen Pressen für die Probenvorbereitung?Präzise, gleichmäßige Proben für eine zuverlässige Analyse
- Welche Bedeutung haben hydraulische Pressen in Laboratorien? Erschließen Sie Präzision und Leistung für Ihre Forschung
