Was Sind Matrixeffekte Bei Der Röntgenfluoreszenzanalyse (Rfa)? Meistern Sie Genaue Elementanalysen Mit Bewährten Korrekturmethoden

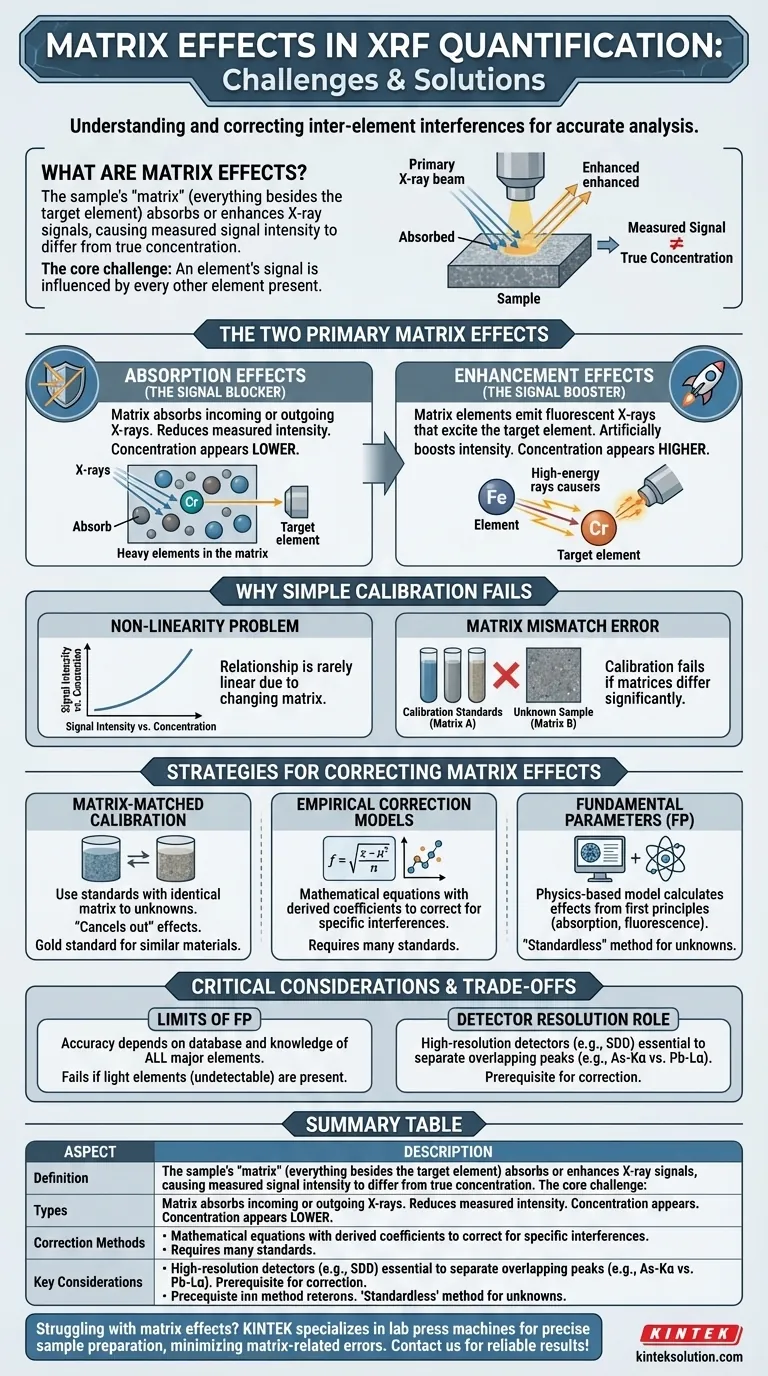
Bei der Röntgenfluoreszenzanalyse (RFA) handelt es sich bei Matrixeffekten um inter-elementare Störungen innerhalb einer Probe, die dazu führen, dass das gemessene Signal eines Elements von seiner tatsächlichen Konzentration abweicht. Die „Matrix“ – also alles in der Probe außer dem spezifisch gemessenen Element – kann die Röntgenstrahlen entweder absorbieren oder die Fluoreszenzsignale verstärken, was bei fehlender Korrektur zu erheblichen Quantifizierungsfehlern führt.

Die Kernherausforderung der RFA besteht darin, dass das Signal eines Elements nicht unabhängig ist; es wird von jedem anderen vorhandenen Element beeinflusst. Um diese Matrixeffekte genau zu überwinden, müssen entweder perfekt angepasste Kalibrierstandards verwendet oder hochentwickelte Softwaremodelle eingesetzt werden, um diese physikalischen Wechselwirkungen rechnerisch zu korrigieren.

Die zwei Haupttypen von Matrixeffekten

Matrixeffekte sind keine zufälligen Fehler. Es handelt sich um vorhersagbare physikalische Phänomene, die hauptsächlich in zwei Kategorien fallen: Absorption und Enhancement (Verstärkung).

Absorptionseffekte (Der Signalblocker)

Der häufigste Matrixeffekt ist die Absorption. Die Probenmatrix kann sowohl die einfallenden Röntgenstrahlen von der Quelle als auch die von dem interessierenden Element ausgehenden Fluoreszenz-Röntgenstrahlen absorbieren.

Dies geschieht auf zwei Arten. Erstens können schwere Elemente in der Matrix die primären Röntgenstrahlen absorbieren und so die Anzahl der Strahlen reduzieren, die Ihr Ziel-Element erreichen und anregen. Zweitens kann die Matrix die charakteristischen Röntgenstrahlen, die von Ihrem Ziel-Element emittiert werden, absorbieren, bevor diese überhaupt den Detektor erreichen. Beide Effekte reduzieren die gemessene Intensität, wodurch die Konzentration des Elements niedriger erscheint, als sie tatsächlich ist.

Enhancement-Effekte (Der Signalverstärker)

Enhancement, oder sekundäre Fluoreszenz, ist das Gegenteil der Absorption. Dies tritt auf, wenn ein anderes Element in der Matrix Fluoreszenz-Röntgenstrahlen mit genügend Energie abgibt, um Ihr Ziel-Element anzuregen.

Wenn Sie beispielsweise Chrom (Cr) in einer Stahllegierung messen, können die energiereichen Röntgenstrahlen des Eisens (Fe) dazu führen, dass auch die Cr-Atome fluoreszieren. Diese „zusätzliche“ Fluoreszenz addiert sich zum Signal, das von der primären Röntgenquelle erzeugt wird, wodurch die Cr-Intensität künstlich erhöht und seine Konzentration höher erscheint, als sie tatsächlich ist.

Warum einfache Kalibrierung nicht ausreicht

Diese physikalischen Effekte untergraben direkt grundlegende quantitative Methoden, bei denen davon ausgegangen wird, dass die Signalintensität direkt proportional zur Konzentration ist.

Das Problem der Nichtlinearität

Aufgrund von Matrixeffekten ist die Beziehung zwischen der Konzentration eines Elements und seiner gemessenen Röntgenintensität selten eine gerade Linie. Eine Verdoppelung der Menge eines Elements führt nicht notwendigerweise zu einer Verdoppelung seines Signals, wenn sich gleichzeitig die Matrix ändert. Diese Nichtlinearität macht einfache Kalibrierkurven bei Proben mit unterschiedlicher Zusammensetzung unzuverlässig.

Der Fehler der „Matrix-Inkompatibilität“

Dies ist die häufigste praktische Falle. Wenn Sie eine Kalibrierkurve mit einem Satz von Standards mit einem Matrixtyp erstellen (z. B. einfache Metalllegierungen), liefert diese Kalibrierung ungenaue Ergebnisse, wenn sie zur Messung einer Probe mit einem anderen Matrixtyp (z. B. einem Mineralerz, einem Kunststoff oder einem Öl) verwendet wird. Die Absorptions- und Enhancement-Effekte sind zwischen den beiden Probentypen völlig unterschiedlich und machen die Kalibrierung ungültig.

Strategien zur Korrektur von Matrixeffekten

Glücklicherweise gibt es etablierte Methoden, um diese Effekte zu kompensieren und eine genaue quantitative Analyse zu erreichen.

Matrix-angepasste Kalibrierung

Dies ist die direkteste Lösung. Dabei werden Kalibrierstandards erstellt, deren Matrix nahezu identisch mit der der unbekannten Proben ist. Diese Methode „hebt“ die Matrixeffekte effektiv auf, da sie sowohl in den Standards als auch in den Unbekannten gleich sind. Dies ist der Goldstandard für Genauigkeit, aber nur für die Routineanalyse sehr ähnlicher Materialien praktikabel.

Empirische Korrekturmodelle

Diese Modelle verwenden mathematische Gleichungen mit empirisch abgeleiteten Koeffizienten, um den Einfluss spezifischer störender Elemente zu korrigieren. Sie erfordern die Analyse einer großen Anzahl gut charakterisierter Standards, um ein robustes Modell aufzubauen. Sobald sie etabliert sind, können sie jedoch für einen definierten Bereich von Materialtypen sehr effektiv sein.

Fundamentalparameter-Ansatz (FP-Methode)

Die Fundamentalparameter-Methode (FP) ist der leistungsstärkste und flexibelste Ansatz. Anstatt sich auf Standards zu verlassen, verwendet FP ein physikbasiertes Modell, um die Matrixeffekte aus den ersten Prinzipien zu berechnen. Die Software verwendet grundlegende Konstanten – wie Absorptionskoeffizienten und Fluoreszenzausbeuten –, um vorherzusagen, wie Röntgenstrahlen mit der Zusammensetzung der Probe interagieren werden. Diese „standardlose“ Methode ist ideal für die Analyse unbekannter oder stark variierender Proben, bei denen die Erstellung angepasster Standards unmöglich ist.

Verständnis der Kompromisse und Fallstricke

Obwohl Korrekturmethoden leistungsstark sind, haben sie Einschränkungen, die für eine zuverlässige Analyse unbedingt verstanden werden müssen.

Die Grenzen der Fundamentalparameter

Der FP-Ansatz ist nicht unfehlbar. Seine Genauigkeit hängt von der Qualität seiner physikalischen Datenbank und insbesondere von der Annahme ab, dass die Software alle Hauptelemente in der Probe kennt. Wenn ein signifikanter Teil der Matrix aus leichten Elementen (wie Kohlenstoff, Sauerstoff oder Stickstoff) besteht, die das RFA-Gerät nicht nachweisen kann, basiert das FP-Modell auf einer unvollständigen Grundlage und seine Korrekturen werden ungenau sein.

Die Rolle der Detektorauflösung

Bevor Matrixeffekte korrigiert werden können, muss das Signal eines Elements sauber gemessen werden können. Dies kann durch eine schlechte Detektorauflösung beeinträchtigt werden, die zu spektralen Peaküberlappungen führt. Beispielsweise liegt der Arsen (As) K-alpha-Peak sehr nahe am Blei (Pb) L-alpha-Peak. Ein Detektor mit geringer Auflösung kann sie nicht trennen, wodurch es unmöglich wird, für eines der beiden eine genaue Intensität zu erhalten.

Moderne Detektoren mit hoher Auflösung, wie Siliziumdrift-Detektoren (SDD), sind unerlässlich, um diese überlappenden Peaks zu trennen. Eine genaue Peakidentifizierung ist eine Voraussetzung für jede erfolgreiche Matrixkorrektur.

Auswahl des richtigen Ansatzes für Ihre Analyse

Ihr analytisches Ziel bestimmt die beste Strategie für den Umgang mit Matrixeffekten.

Wenn Ihr Hauptaugenmerk auf der Qualitätskontrolle eines bekannten Materials liegt: Matrix-angepasste Standards bieten die höchste Genauigkeit und Wiederholbarkeit.
Wenn Ihr Hauptaugenmerk auf der Analyse vielfältiger und unbekannter Proben liegt: Der Fundamentalparameter-Ansatz (FP) bietet die größte Flexibilität und ist oft die einzig praktikable Option.
Wenn Sie Spurenelemente neben Hauptelementen messen: Stellen Sie sicher, dass Ihr System über einen Detektor mit hoher Auflösung verfügt, um Peaküberlappungen zu vermeiden, noch bevor Sie eine Matrixkorrektur in Betracht ziehen.

Das Verständnis und die Korrektur von Matrixeffekten sind der Schlüssel, um die RFA von einem qualitativen Screening-Werkzeug in ein präzises quantitatives Instrument zu verwandeln.

Zusammenfassungstabelle:

Aspekt	Beschreibung
Definition	Inter-elementare Störungen bei der RFA, die die Signalintensität von der tatsächlichen Konzentration abweichen lassen.
Typen	Absorption (reduziert Signal) und Enhancement (verstärkt Signal).
Korrekturmethoden	Matrix-angepasste Kalibrierung, Empirische Modelle, Fundamentalparameter (FP).
Wichtige Überlegungen	Erfordert Detektoren mit hoher Auflösung für eine genaue Peak-Trennung und vollständige Elementkenntnis für FP.

Haben Sie Schwierigkeiten mit Matrixeffekten bei Ihrer RFA-Analyse? KINTEK ist spezialisiert auf Laborpressen, einschließlich automatischer, isostatischer und beheizter Laborpressen, die zur Unterstützung einer präzisen Probenvorbereitung für eine genaue RFA-Quantifizierung entwickelt wurden. Unsere Geräte helfen, matrixbedingte Fehler durch Gewährleistung einer gleichmäßigen Probenkonsistenz zu minimieren, was zu zuverlässigen Ergebnissen in der Qualitätskontrolle und Forschung führt. Steigern Sie die Effizienz Ihres Labors – kontaktieren Sie uns noch heute, um zu besprechen, wie unsere Lösungen Ihren spezifischen Anforderungen zugutekommen können!